Learning Hybrid Process Models From Events¶
Ref :
Aalst, Wil M. P. van der, Riccardo De Masellis, Chiara Di Francescomarino and Chiara Ghidini. “Learning Hybrid Process Models from Events - Process Discovery Without Faking Confidence.” (2017).
Summary¶
Event logs often contains incomplete and infrequent behaviours, creating complex dependencies with formal semantics. Removing these outliers can result in a simpler process model. But instead of leaving out the weak or complex dependencies, they can also be depicted in an informal manner.
The central idea in a hybrid miner is to have formal semantics for strong causal relation whenever there is enough structure and evidence in the data, and model other relations using informal semantics with different types of arcs indicating level of certainity.
Hybrid petri net $HPN = (P,T,F_1, F_2, F_3)$
Where,
$P $: set of places
$T $: set of transitions
$F_1 $: Normal petrinet arcs connecting activities through places, $F_1 \subseteq (P \times T) \cup (T \times P)$
$F_2 $: Strong causalities with arcs directly connecting transitions (sure arcs), $F_2 \subseteq T \times T$
$F_3 $: Weak causalities with arcs directly connecting transitions (unsure arcs), $F_3 \subseteq T \times T$
Discovering Hybrid process models¶
Discovering HPN involves finding all the arcs and places in the above formalism
1) Build the causal graph and classify the causalities as strong or weak
Causal graph $G = (\mathbf{\Sigma}, R_S, R_W)$
Where,
$\mathbf{\Sigma}$ : Set of all activities including unique start and end activity
$R_S \subseteq \mathbf{\Sigma} \times \mathbf{\Sigma}$ : Set of strong causal relations
$R_W \subseteq \mathbf{\Sigma} \times \mathbf{\Sigma}$ : Set of weak causal relations
$R_S \cup R_W = \phi$
Let $L \in \mathcal{B}(\mathbf{\Sigma}^+)$ and $\{a,b\} \subseteq \mathbf{\Sigma}$
Compute $Rel_1(a,b,L)$ which counts the strength of relation (a,b) relative to XOR-split and joint behaviour
$Rel_1(a,b,L) = \cfrac{2 \times \#(a \to b)}{\#(a \to *) + \#(* \to b)}$
Compute $Rel_2(a,b,L)$ to take into account concurrency and loops
$ Rel_2(a,b,L) = \begin{cases} \cfrac{\#(a \to b) - \#(b \to a)}{\#(a \to b) + \#(b \to a) + 1} & \quad \text{if } \#(a \to b) - \#(b \to a) \gt 0\\ \\ \cfrac{\#(a \to b)}{\#(a \to b) + 1} & \quad \text{if } a=b\\ \\ 0 & \quad \text{otherwise} \end{cases}$
Quantify causal relation $Caus_w(a,b,L)$
$Caus_w(a,b,L) = w.Rel_1 + (1-w).Rel_2 \qquad$ Where $w \in [0,1]$
Effect of $w$ : Setting $w=0$ boosts the quantification of concurrent and loop relations, and makes the resulting process model more complex. I see $w$ as a parameter that controls the complexity of process model in terms of concurrency and loops
Let $\mathbf{\Sigma'}$ be set of all activities occuring atleast $t_{freq}$ times (start and end activities are always included)
Now we can classify the causal relations as strong or weak
$R_S = \{(a,b) \in \mathbf{\Sigma'} \times \mathbf{\Sigma'} \ \mid \ Caus_w(a,b,L\upharpoonright_{\mathbf{\Sigma'}}) \geq t_{Rs}\} $
$R_W = \{(a,b) \in \mathbf{\Sigma'} \times \mathbf{\Sigma'} \ \mid \ Caus_w(a,b,L\upharpoonright_{\mathbf{\Sigma'}}) \geq t_{Rw}\} $
$t_{Rs} \geq t_{Rw}$
2) Generate candidate places on relations in set $R_S$ and evaluate using replay techniques. Then,
$F_1 $: Strong causalities($\in R_S$) that can be expressed in terms of places
$F_2 $ = Strong causalities($\in R_S$) that cannot be expressed in terms of places
$F_3 = R_W$
Let set of candidate places be $\{ p=(I,O) \ \mid \ I \neq \phi \ \cap \ O \neq \phi \ \cap \ I\times O \subseteq R_S \}$
Where
$\bullet p = I$ is the set of input transitions to place P
$p \bullet = O$ is the set of output transitions from place P
Compute the score for each candidate place, considering the fraction of fitting traces
Recall that adding places will inhibit behaviour
Eg. Adding places with $\bullet p1, \bullet p2 = \{a\}$, $ p1 \bullet = \{b\}$, $ p2 \bullet = \{c\}$ in the following petrinet will now force the behaviour to contain both b and c (i.e trace < a,c > will no longer fit)
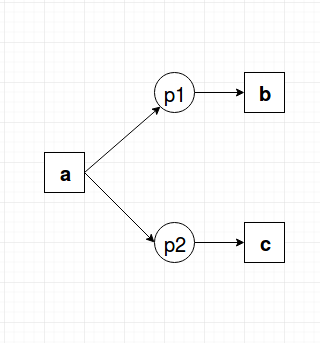
Therefore, if a place p does not inhibit a trace $\sigma$, then the following conditions will be satisfied
1) Check correctness at AND-Splits: $ \mid\{ 1 \leq i \le |\sigma| \mid a_i \in I\} \mid \ = \ \ \mid\{ 1 \leq i \leq |\sigma| \mid a_i \in O\} \mid $
2) Check correctness at XOR-Splits: $\forall k \in \{1,..,|\sigma|\}: \ \mid\{ 1 \leq i \le k \mid a_i \in I\} \mid \ \geq \ \ \mid\{ 1 \leq i \leq k \mid a_i \in O\} \mid $
A place that satisfy the above conditions is called a replayable trace w.r.t to place p and is denoted as $\checkmark(p,\sigma)$
Now every candidate places can be scored in terms of replayable traces
$score(p,L) \ = \ \cfrac{\mid \sigma \in L \ \mid \ \checkmark(p,\sigma) \ s.t \ \exists_{a \in \sigma} a \in (I\cup O) \ \mid}{\mid \sigma \in L \ \mid \ \ \exists_{a \in \sigma} a \in (I\cup O) \ \mid}$
which quantifies the fraction of replayable traces that have been activated
If this score is greater than certain threshold $t_{replay}$, then the corresponding place is added to the process model
$Q = \{p \ \mid \ score(p,L\upharpoonright_{\mathbf{\Sigma'}}) \geq t_{replay}\}$
Arcs $F_1$ can be formalized from $Q$.
$F_2$ is then the remaining arcs with strong causality without places
Thus we have computed all the parameters required for a Hybrid process model
Effect of hyper-parameters on fitness and precission¶
Remember, when number of places increases (simplicity reduces), fitness decreases and precission increases. (and vice versa)
1) $t_{replay}$ is less $\implies$ more places are added $\implies$ fitness decreases and precission increases
2) $t_{Rs}$ is less $\implies$ more strong relations (or more candidate places) $\implies$ chances for more places to be added $\implies$ fitness decreases and precission increases
3) $w$ is less $\implies$ loops and concurrent relations have high causality score $\implies$ more strong relations (or more candidate places) $\implies$ chances for more places to be added $\implies$ precission increases